Cách tính đường chéo hình thoi. Ví dụ minh họa dễ hiểu

Tính đường chéo của hình thoi là một trong những kỹ năng cơ bản và quan trọng trong toán hình học. Đường chéo của hình thoi không chỉ giúp xác định diện tích mà còn là yếu tố quan trọng giúp hiểu được tính chất của hình thoi.

Trong bài viết này Fresh Lemon Review sẽ hướng dẫn các bạn những phương pháp đơn giản, dễ hiểu để tính độ dài đường chéo của hình thoi. Thông qua các ví dụ minh họa chi tiết, bạn sẽ nắm vững cách áp dụng công thức và thực hiện các bước tính toán một cách chính xác.

Các cách tính đường chéo của hình thoi

Hình thoi là một tứ giác đặc biệt trong hình học, có các đặc điểm sau:

• Bốn phía đều bình đẳng.
• Các góc đối diện bằng nhau.
• Các đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường chéo.

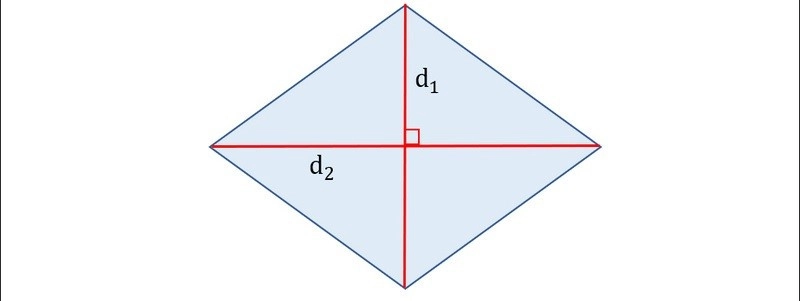
Các đường chéo của hình thoi là hai đoạn thẳng nối các đỉnh đối diện của hình thoi. Đặc điểm của đường chéo kim cương bao gồm:

• Hai đường chéo cắt nhau tại một điểm và chia hình thoi thành bốn hình tam giác vuông.
• Các đường chéo vuông góc với nhau (góc 90 độ).
• Giao điểm của hai đường chéo là trung điểm của mỗi đường chéo, nghĩa là mỗi đường chéo này chia đôi đường chéo kia.

shình thoi

Có nhiều cách tính đường chéo của hình thoi, tùy thuộc vào thông tin đã biết về hình thoi. Dưới đây là một số cách phổ biến nhất:

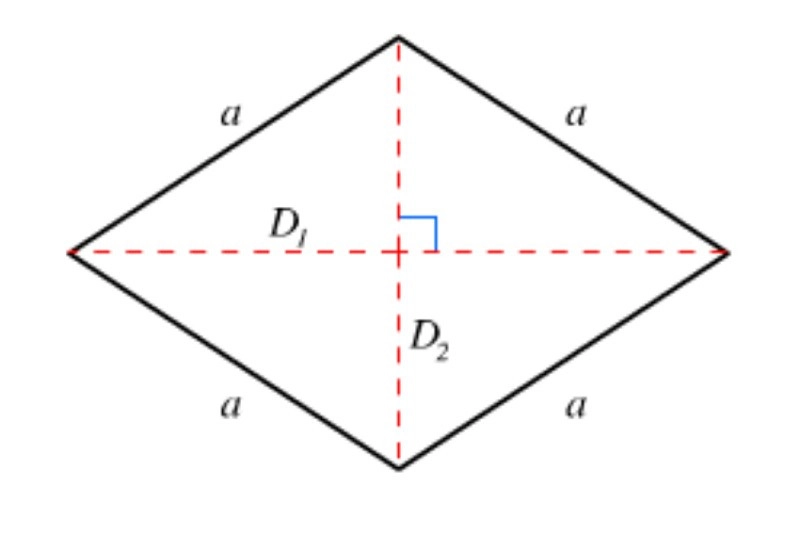
1. Tính đường chéo khi biết độ dài hai cạnh của hình thoi

Theo định lý Pytago cho tam giác vuông tạo bởi một đường chéo và một nửa cạnh của hình thoi, ta có:

d^2 = (p/2)^2 + (q/2)^2 => d=√(p^2+q^2)

Công thức:

d=√(p^2+q^2)​

Trong đó:

• d là chiều dài đường chéo
• p và q là độ dài hai cạnh của hình thoi

Ví dụ: Một hình thoi có hai cạnh lần lượt là 4 cm và 3 cm. Tính độ dài đường chéo của hình thoi.

Áp dụng công thức trên, ta có: d=√(4^2+3^2​) cm

=> d=5 cm

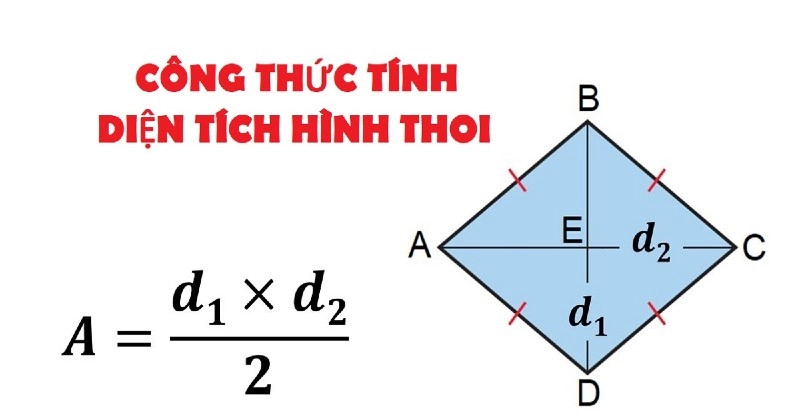
2. Cách tính đường chéo hình thoi khi biết diện tích

Ta có công thức tính diện tích hình thoi: S = (d*d2)/2 => d=​(2xS)/d2

Công thức:

d=​(2xS)/d2​

Trong đó:

• d là độ dài đường chéo cần tính
• S là diện tích hình thoi
• d2​ là độ dài đường chéo đã biết

Ví dụ: Một hình thoi có diện tích là 20 cm2 và đường chéo là 8 cm. Tính độ dài đường chéo còn lại.

Áp dụng công thức trên ta có: d= 2×20/8

=> d=5 cm

Từ S đến d

3. Tính đường chéo khi biết chu vi hình thoi

Công thức:

d=C/2​

Trong đó:

• d là chiều dài đường chéo
• C là chu vi của hình thoi

Ví dụ: Một hình thoi có chu vi là 20cm. Tính độ dài đường chéo của hình thoi.

Áp dụng công thức trên ta có: d=20/2​ cm

=> d=10 cm

Một số bài tập minh họa có đáp án

Hình vẽ minh họa các bài viết

Bài 1: Cho một hình thoi có diện tích 36 cm2, đường chéo dài 6 cm. Tính độ dài đường chéo còn lại.

Phần thưởng:

Gọi độ dài đường chéo còn lại của hình thoi d.

Ta có: d=2×36/6

=> d = 12cm

Vậy độ dài đường chéo còn lại của hình thoi là 12 cm.

Bài 2: Một hình thoi có hai đường chéo có độ dài lần lượt là 8 cm và 10 cm. Tính độ dài cạnh của hình thoi.

Phần thưởng:

Gọi độ dài cạnh của hình thoi là a.

Theo định lý Pytago cho tam giác vuông tạo bởi một đường chéo và một nửa cạnh của hình thoi, ta có:

a^2 = (d1/2)^2 + (d2/2)^2

Thay số vào, ta được:

a^2 = (8 / 2)^2 + (10 / 2)^2

Giải phương trình, ta được:

một = 6 cm

Vậy độ dài cạnh của hình thoi là 6 cm.

Bài 3: Một mảnh đất hình thoi có diện tích là 600 m2, chiều dài đường chéo lớn hơn chiều dài đường chéo nhỏ là 20 m. Tính diện tích mảnh đất.

Phần thưởng:

Gọi chiều dài đường chéo nhỏ của mảnh đất là d1 và chiều dài đường chéo lớn là d2.

Theo đề bài ta có:

d2 = d1 + 20

Diện tích thửa đất hình thoi được tính theo công thức:

S = (d1 * d2) / 2

Thay số vào, ta được:

600 = (d1 * (d1 + 20)) / 2

Giải phương trình, ta được:

d1 = 40 cmd2 = 60 cm

Diện tích mảnh đất hình thoi là:

S = (d1 * d2) / 2 = (40 * 60) / 2 = 1200 cm²

Vậy diện tích mảnh đất là 1200 cm2.

Bài 4: Một hình thoi có diện tích 100 cm2 và có góc nhọn bằng 60 độ. Tính diện tích của hình thoi.

Phần thưởng:

Gọi độ dài cạnh của hình thoi là a.

Chúng ta có thể chia hình thoi thành hai hình tam giác vuông bằng nhau. Gọi độ dài đường cao tương ứng với cạnh huyền của mỗi tam giác vuông là h.

Theo định lý sin trong tam giác vuông, ta có:

tội lỗi 60° = h/a

=> h = a * √3 / 2

Diện tích của mỗi tam giác vuông được tính theo công thức:

S = (a*h)/2

Vì diện tích hình thoi bằng tổng diện tích của hai tam giác vuông nên ta có:

Diện tích hình thoi = 2*(a*h)/2=a*h

Thay h vào, ta được:

Diện tích hình thoi = a * (a * √3/2) = a² * √3/2

Theo bài toán, diện tích hình thoi là 100 cm2, ta có phương trình: a² * √3/2 = 100

Giải phương trình ta được: a = 10 cm

Vậy diện tích hình thoi là:

Diện tích hình thoi = a² * √3/2 = 10² * √3/2 = 50√3 cm²

Đáp án: 50√3 cm2.

Qua bài viết này hy vọng các bạn đã nắm vững các phương pháp, công thức cần thiết để tính độ dài đường chéo của hình thoi. Ví dụ minh họa cụ thể giúp làm rõ các bước và cách áp dụng kiến ​​thức vào thực tế. Khi hiểu rõ cách tính đường chéo, bạn sẽ dễ dàng giải các bài toán liên quan đến hình thoi một cách chính xác và hiệu quả. Nếu bạn vẫn còn thắc mắc về cách tính đường chéo của hình thoi, hãy để lại bình luận để mình giải đáp nhé!