Công thức tính diện tích hình bình hành & các dạng bài tập

Bạn có muốn hiểu cách tính diện tích hình bình hành không? Đây là kiến ​​thức toán học quan trọng, không chỉ cho học tập mà còn có nhiều ứng dụng thực tế trong cuộc sống. Có thể bạn đã quên hoặc cần ôn lại kiến ​​thức về công thức tính diện tích hình bình hành? Đừng lo lắng, trong bài viết này Fresh Lemon Review sẽ giúp bạn hiểu rõ và ghi nhớ những chi tiết quan trọng, đồng thời đưa ra những gợi ý tính toán cụ thể. Hãy cùng tìm hiểu ngay bây giờ!

Hình bình hành là gì?

Hình bình hành trong hình học Euclide là một tứ giác được hình thành khi hai cặp đường thẳng song song cắt nhau. Đây là một biến thể đặc biệt của hình thang, bao gồm 4 góc và có những đặc điểm giống nhau với cả hình thang và hình chữ nhật.

Trong không gian 3 chiều, hình bình hành tương đương là hình lục giác.

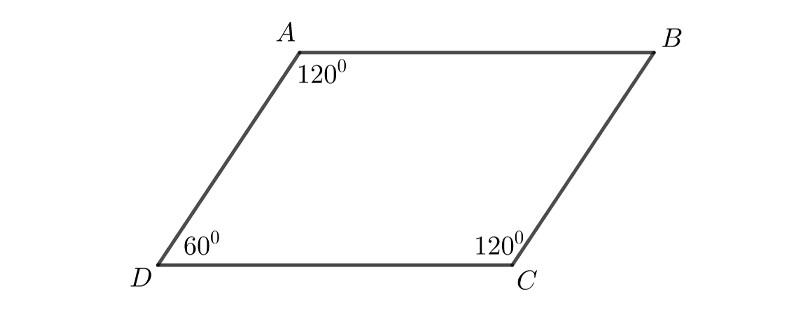Hình bình hành ABCD

Tính chất của hình bình hành

Hình bình hành có một số tính chất đáng chú ý, bao gồm:

• Các cặp cạnh đối diện song song và bằng nhau.
• Tổng độ dài hai đường chéo của hình bình hành bằng tổng độ dài bốn cạnh của nó. Các góc đối diện bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường
• Hai đường chéo của hình bình hành cắt nhau tại trung điểm và chia hình bình hành thành hai hình tam giác đồng dạng.
• Giao điểm của hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.

Dấu hiệu nhận biết hình bình hành

1. Hình bình hành là tứ giác đặc biệt

• Tứ giác có hai cặp cạnh song song được coi là một loại hình bình hành.
• Trong một tứ giác, khi có hai cặp cạnh đối diện bằng nhau thì chúng ta cũng có thể coi đó là hình bình hành.
• Nếu một tứ giác có các cặp cạnh đối song song và bằng nhau thì chúng ta có thể coi đó là hình bình hành.
• Một tứ giác có hai cặp góc đối diện bằng nhau cũng có thể được coi là hình bình hành.
• Khi một tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường thẳng thì đó cũng là một loại hình bình hành.

2. Hình bình hành là hình thang

• Hình thang có hai cạnh đáy bằng nhau là hình bình hành.
• Hình thang có hai cạnh song song là hình bình hành

Công thức tính diện tích hình bình hành

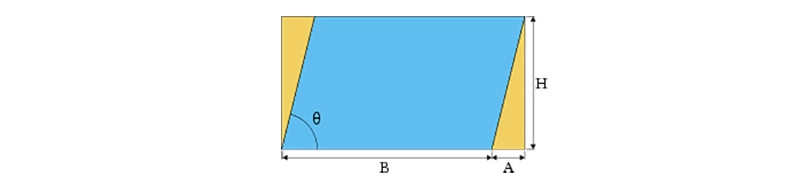Hình bình hành: Công thức tính diện tích hình bình hành

Nhanh tay áp dụng Tính diện tích hình bình hành trực tuyến, các bạn có thể copy và dán link tìm kiếm sau: https://giaitoannhanh.com/dien-tich-hinh-binh-hanh/.

Công thức 1: Diện tích hình bình hành

Công thức tính diện tích hình bình hành được phát biểu như sau: Diện tích hình bình hành bằng độ dài cạnh đáy nhân với chiều dài chiều cao.

Gọi B là độ dài cạnh đáy, H là chiều dài chiều cao và S là diện tích. Chúng ta có công thức:

S = B x H

Công thức 2: Diện tích hình bình hành

Ngoài công thức trên, bạn cũng có thể áp dụng công thức sau để tính diện tích hình bình hành: Diện tích hình bình hành bằng tích độ dài 2 cạnh kề nhân với sin của góc do 2 cạnh đó tạo thành.

Gọi A và B lần lượt là độ dài hai cạnh và góc a là góc nối hai cạnh A và B.

S = A x B x sin a

Cách tính chiều cao của hình bình hành

Chiều cao của hình bình hành bằng diện tích chia cho đáy.

H = S : A

• Trong đó S là diện tích, A là đáy và H là chiều cao.

Cách tính đáy của hình bình hành

Cạnh đáy của hình bình hành bằng diện tích chia cho chiều cao.

A = S : H

• Trong đó S là diện tích, A là đáy và H là chiều cao.

Công thức tính diện tích hình thoi

Hình thoi là một dạng đặc biệt của hình bình hành vì nó có tất cả các tính chất của hình bình hành và ngoài ra còn có một số tính chất khác:

• Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc là hình thoi.
• Hình bình hành có đường chéo là đường phân giác của một góc là hình thoi.

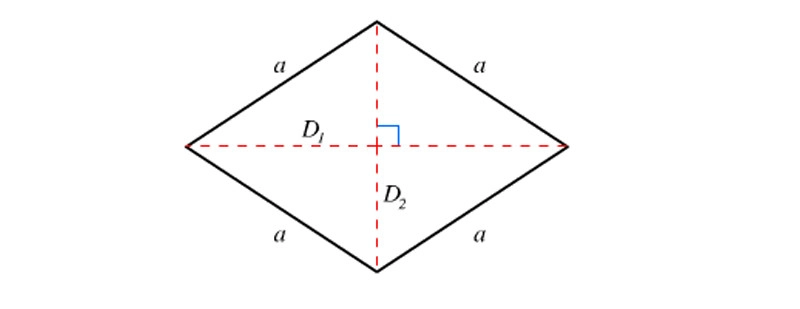Diện tích hình bình hành đặc biệt: hình thoi

Công thức tính diện tích hình thoi bằng một nửa tích độ dài hai đường chéo.

S = 1/2x(D1xD2)

Chu vi hình thoi bằng độ dài một cạnh nhân với 4.

P = rìu 4

Công thức tính chu vi hình bình hành

Công thức tính chu vi hình bình hành

Chu vi của hình bình hành bằng hai lần tổng của bất kỳ cặp cạnh kề nào.

P = (a + b) x 2

Lưu ý khi tính diện tích hình bình hành

Dưới đây là một số lưu ý khi tính diện tích hình bình hành mà bạn cần biết:

Dưới đây là một số điều cần nhớ khi tính diện tích hình bình hành:

• Đơn vị đo chiều dài: Đảm bảo cả đáy và chiều cao đều được đo bằng cùng một đơn vị để tránh nhầm lẫn.
• Kiểm tra kết quả: Luôn kiểm tra ít nhất hai lần để đảm bảo tính chính xác và tránh sai sót.
• Công thức đúng: Sử dụng công thức phù hợp với yêu cầu của bài toán để đạt được kết quả chính xác.

Các dạng bài tập tính diện tích hình bình hành

Dạng 1: Tính diện tích khi biết chiều dài đáy và chiều cao

Giải: Với dạng bài tập này, bạn chỉ cần áp dụng công thức tính diện tích S = B x H để tính ra kết quả cuối cùng.

Bài tập ví dụ: Tính diện tích hình bình hành có chiều dài đáy 8 cm và chiều cao 10 cm.

Giải: Áp dụng công thức S = B x H ta có: S = 8 x 10 = 80 cm²

Vậy diện tích hình bình hành là 60 cm2.

Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao của hình bình hành

Lời giải: Từ công thức chuẩn S = B x H, ta suy ra công thức tính độ dài cơ sở như sau: B = S : H.

Bài tập ví dụ: Tính chiều dài đáy của hình bình hành có diện tích 50 cm2 và chiều cao 5 cm.

Lời giải: Từ công thức S = B x H, ta suy ra công thức tính độ dài đáy: B = S : H.

Thay vào đó: S = 50 cm²; H = 5cm

Ta có: B = S : H = 50 : 5 = 10 cm

Vậy độ dài cạnh đáy của hình bình hành là 8 cm.

Dạng 3: Tính chiều cao khi biết diện tích và chiều dài đáy của hình bình hành

Giải: Từ công thức S = B x H ta suy ra công thức tính chiều cao của hình là H = S : B

Bài tập ví dụ: Tính chiều dài đáy của hình bình hành có diện tích 60 cm2 và chiều cao 5 cm.

Lời giải: Từ công thức S = B x H, ta suy ra công thức tính độ dài đáy: B = S : H.

Thay vào đó: S = 60 cm²; h = 5cm

Ta có: H = S : B = 70 : 7 = 10cm

Vậy độ dài cạnh đáy của hình bình hành là 10 cm.

Dạng 4: Tính diện tích hình bình hành khi biết diện tích hình chữ nhật và diện tích tam giác tạo thành nó

Giải: Trước tiên, hãy xét xem diện tích của hai hình có cùng đơn vị đo hay không. Nếu không thì đổi sang đơn vị đo diện tích tương tự. Sau đó dùng phép tính tổng để tính diện tích hình bình hành.

Bài tập ví dụ: Tính diện tích hình bình hành khi biết diện tích hình chữ nhật và hình tam giác tạo nên nó gồm: Diện tích hình chữ nhật S1 = 10 cm²; Diện tích tam giác S2 = 600 mm²

Lời giải: Ta có Diện tích tam giác S2 = 600 mm² = 6 cm²

Diện tích hình bình hành: S = S1 + 2 x S2 = 10 + 2 x 6 = 10 + 12 = 22 cm²

Tổng hợp các bài tập tự luyện tại nhà

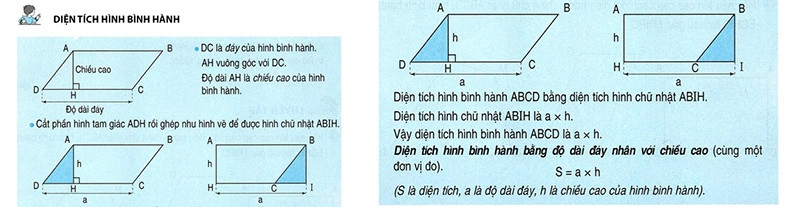Bài tập tính diện tích hình bình hành

Câu 1: Tính diện tích hình bình hành có chiều dài đáy 10cm và chiều cao 6m.

Câu 2: Một mảnh đất hình bình hành có chiều dài đáy là 50dm, chiều cao là 25dm. Tính diện tích mảnh đất đó.

Câu 3: Một thửa đất trồng hoa có hình bình hành, chiều dài đáy là 30 m, chiều cao gấp đôi chiều dài đáy. Tính diện tích mảnh đất trồng hoa.

Câu 4: Một tấm kính hình bình hành có chiều dài 300mm, chiều cao 15cm. Tính diện tích tấm kính đó.

Câu 5: Hình bình hành ABCD có chiều cao 8cm, chiều dài đáy gấp 3 lần chiều cao. Diện tích hình bình hành ABCD tính bằng cm2 là bao nhiêu?

Câu 6: Tính diện tích hình bình hành, biết tổng chiều dài đáy và chiều cao là 24cm, chiều dài đáy hơn chiều cao 4cm.

Câu 7: Một hình bình hành có diện tích là 24cm2, chiều dài đáy là 6cm. Tính chiều cao của hình bình hành đó.

Câu 8: Một hình bình hành có diện tích là 2m2, chiều dài đáy là 20dm. Tính chiều cao của hình bình hành đó.

Câu 9: Hình bình hành có diện tích bằng diện tích hình vuông có cạnh 4cm, chiều cao 2cm. Tính độ dài đáy của hình đó.

Câu 10: Một hình bình hành có chiều cao là 9dm. Tính độ dài đáy của hình đó biết diện tích của nó là 54 dm2.

Xem thêm các bài viết liên quan:

• Công thức tính diện tích hình thang chính xác nhất
• Công thức tính diện tích hình tam giác chính xác nhất

Như vậy, Fresh Lemon Review vừa chia sẻ đến các bạn đặc điểm của hình bình hành và công thức tính diện tích hình bình hành. Bạn có thể áp dụng các công thức để giải các bài toán một cách chính xác nhé!