Công thức tính diện tích hình thang thường, vuông, cân chính xác nhất

Bạn đang tìm công thức tính diện tích hình thang? Đây là khái niệm, kiến ​​thức toán học quan trọng cần thiết cho quá trình học tập của học sinh lớp 5, lớp 6 cũng như quá trình vận dụng vào thực tế sau này. Có thể bạn đã quên hoặc mắc lỗi trong công thức tính toán? Hãy cùng theo dõi bài viết hôm nay của Chánh Tươi Review để cùng tìm hiểu và ghi nhớ chi tiết cũng như gợi ý những phép tính cụ thể nhé!

Hình thang là hình gì?

Hình thang là một dạng hình học thông dụng, là tứ giác lồi có hai cạnh đối song song gọi là cạnh đáy, hai cạnh còn lại là cạnh bên.

Diện tích của hình thang là toàn bộ mặt phẳng bên trong bốn cạnh của nó.

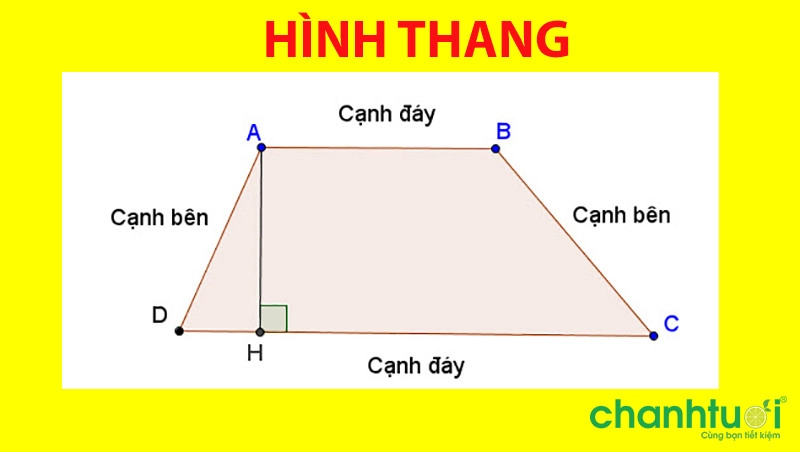Một ví dụ về hình thang là gì

Hình thang có nhiều loại khác nhau, bao gồm:

• Hình thang vuông: có một góc vuông.
• Hình thang cân: có hai góc bằng nhau kề với một đáy.
• Hình bình hành: có hai cạnh đáy bằng nhau và hai cạnh đối song song và bằng nhau.
• Hình chữ nhật: là hình thang vừa vuông vừa cân.

Mỗi loại hình thang có những đặc điểm riêng biệt và được xác định bởi các đặc tính đặc trưng của nó.

XEM SHOP CHUYÊN DỤNG CỤ HỌC TẬP UY TÍN TẠI ĐÂY

Công thức tính diện tích hình thang chính xác nhất

Để giải bài toán tính diện tích hình thang, bạn cần biết công thức tính nhanh và chính xác nhất. Điều này giúp bạn tránh tính toán sai hoặc thiếu số lượng cần thiết để tính diện tích. Vậy công thức tính diện tích hình thang là gì? Hãy cùng Chánh Tươi Review tìm hiểu ngay nhé!

Để tính diện tích hình thang cần những điều kiện gì?

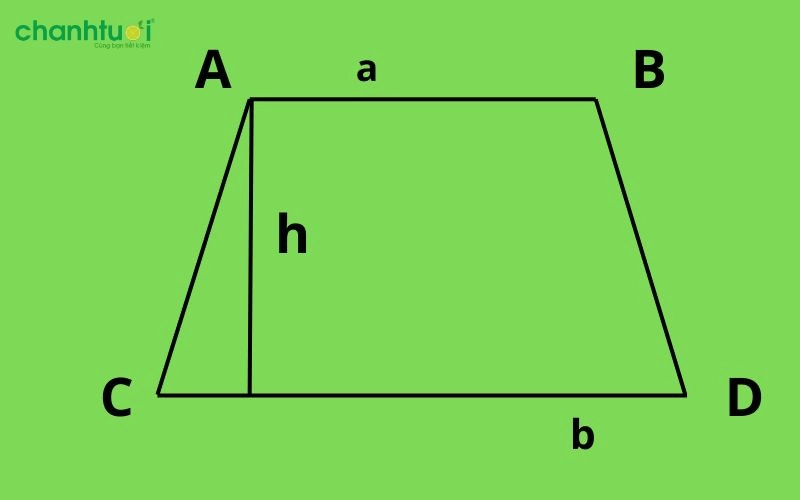
Để tính diện tích hình thang, chúng ta cần xác định các thông số sau:

• Đế nhỏ (ký hiệu a): Đây là cạnh ngắn hơn của hình thang, cũng được đặt nằm ngang và đóng vai trò là đáy dưới.
• Đế lớn (ký hiệu b): Đây là cạnh dài hơn của hình thang, đặt nằm ngang và đóng vai trò là đáy trên.
• Chiều cao (ký hiệu là h): Đây là đoạn thẳng vuông góc với cả hai đáy, nối hai đỉnh không kề nhau của hình thang.

Sau khi xác định đầy đủ các thông số trên, chúng ta có thể dễ dàng áp dụng công thức tính diện tích hình thang.

Hiển thị hình minh họa và ký hiệu để dễ hình dung hơn.

Cần có các điều kiện sau để tính diện tích hình thang

• Hình thang: ABCD
• Đáy nhỏ: a
• Đáy lớn: b
• Chiều cao: h

MUA MÁY TÍNH HỌC CASIO FX-580VN TẠI ĐÂY

Công thức tính diện tích hình thang đều

Sau khi có được các tham số là điều kiện để tính diện tích hình thang, các bạn sẽ áp dụng công thức sau để tính diện tích hình thang:

S (diện tích hình thang) = ((đế nhỏ + đáy lớn)/2) x chiều cao = ((a+b)/2) xh

Công thức tương tự: hx ((a+b)/2) = 1/2h x (a+b) = (hx (a+b)) / 2

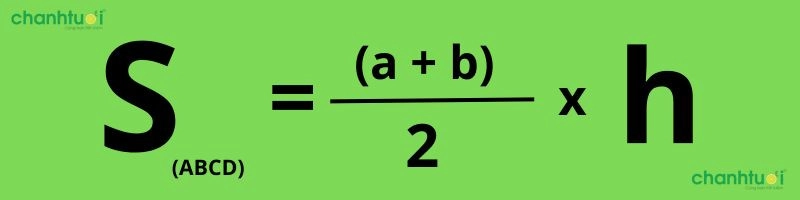Công thức tính diện tích hình thang chính xác

Ví dụ cụ thể: Cho một hình thang có đáy nhỏ a = 4 cm, đáy lớn b = 12 cm và chiều cao h = 6 cm, áp dụng công thức ta có: S = ((4 + 12)/2) x 6 = 48cm2.

Vậy diện tích hình thang là 48 cm2. Công thức này giúp học sinh tính diện tích dễ dàng.

Bài thơ về tính diện tích hình thang:

“Muốn tính diện tích hình thang

Chúng tôi thêm đáy lớn và đáy nhỏ

Sau đó nhân với chiều cao

Chia nó làm đôi và nhận một nửa bất cứ thứ gì bạn muốn.”

Công thức tính diện tích hình thang cân

Hình thang cân là một loại hình thang có hai góc kề nhau có số đo bằng nhau. Đồng thời, hai cạnh của hình thang cân cũng có chiều dài bằng nhau và không chạy song song với nhau.

Ngoài việc áp dụng công thức như tính hình thang thông thường, bạn cũng có thể chia hình thang cân thành những phần nhỏ hơn để tính diện tích từng phần rồi cộng chúng lại với nhau.

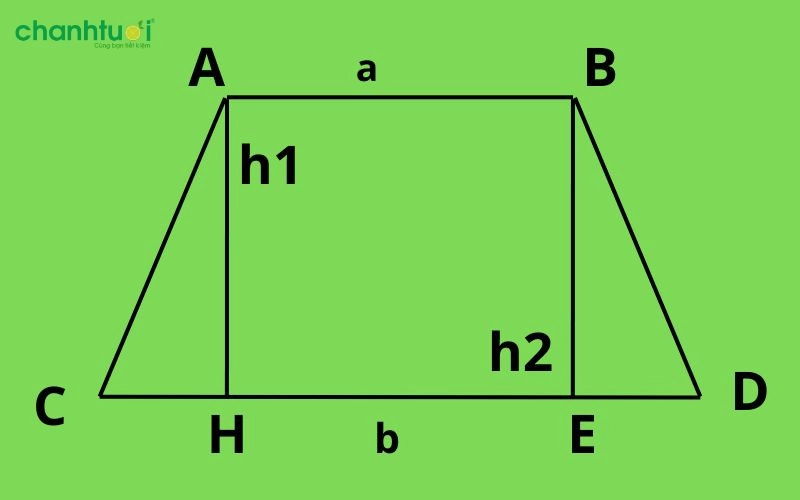Cách tính diện tích hình thang cân

Ví dụ: Hình thang cân ABCD có hai cạnh AC và BD bằng nhau. Với các đường cao AH và BE, hình thang sẽ được chia thành 1 hình chữ nhật ABHE và 2 hình tam giác ACH và BDE. Áp dụng công thức tính diện tích hình chữ nhật cho ABHE và diện tích tam giác cho ACH và BDE sau đó cộng tất cả các diện tích để tìm diện tích hình thang ABCD.

Cụ thể: S(ABCD) = S(ACH) + S(BDE) + S(ABHE) = 2S(ACH) + S(ABHE) = 2S(BDE) + S(ABHE)

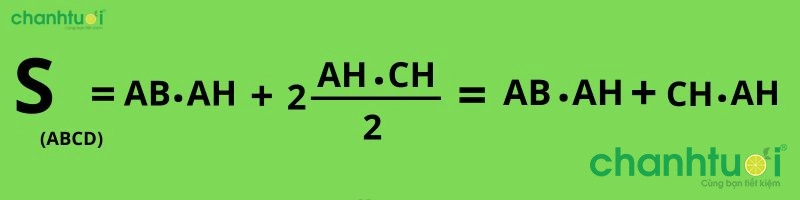Công thức tính diện tích hình thang cân

Công thức tính diện tích hình thang vuông

Hình thang vuông là hình thang có một góc vuông. Cạnh vuông góc với hai đáy cũng là chiều cao h của hình thang.

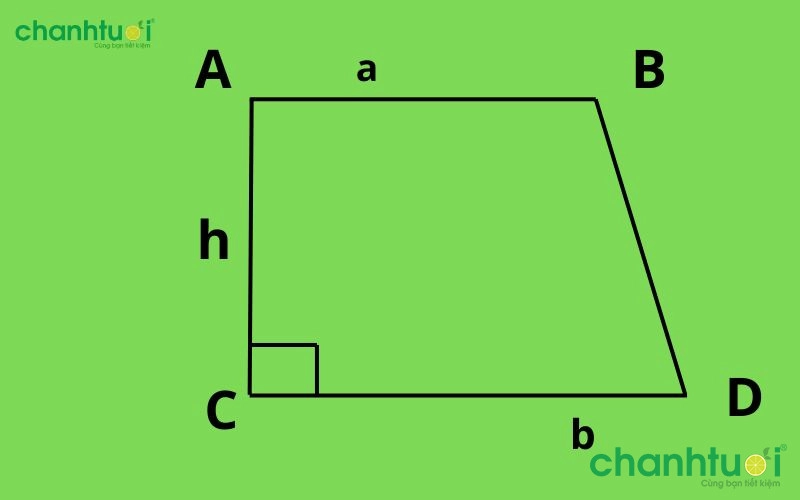Cách tính diện tích hình thang vuông

Công thức chung để tính diện tích hình thang vuông cũng tương tự như hình thang thông thường: trung bình cộng của 2 cạnh đáy nhân với chiều cao giữa 2 đáy, tuy nhiên chiều cao ở đây là cạnh vuông góc với cả hai đáy.

S (diện tích hình thang) = ((đế nhỏ + đáy lớn)/2) x chiều cao = ((a+b)/2) xh

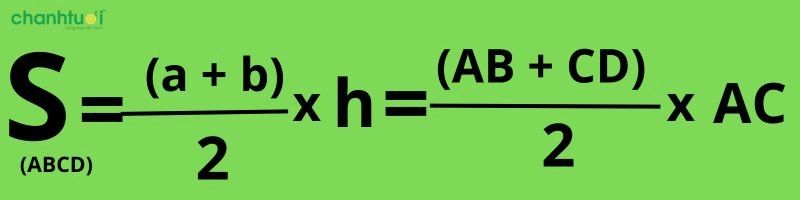Công thức tính diện tích hình thang vuông

Công thức tính diện tích hình bình hành

Hình bình hành là tứ giác được hình thành khi có hai cặp đường thẳng song song. Đây là một biến thể đặc biệt của hình thang, gồm có 4 góc và có chung tính chất với hình thang và hình chữ nhật.

Công thức tính diện tích hình bình hành có thể được biểu diễn như sau:

Diện tích của hình bình hành bằng chiều dài đáy nhân với chiều dài chiều cao. Gọi b là chiều dài cạnh đáy, h là chiều dài chiều cao và S là diện tích: S = bxh

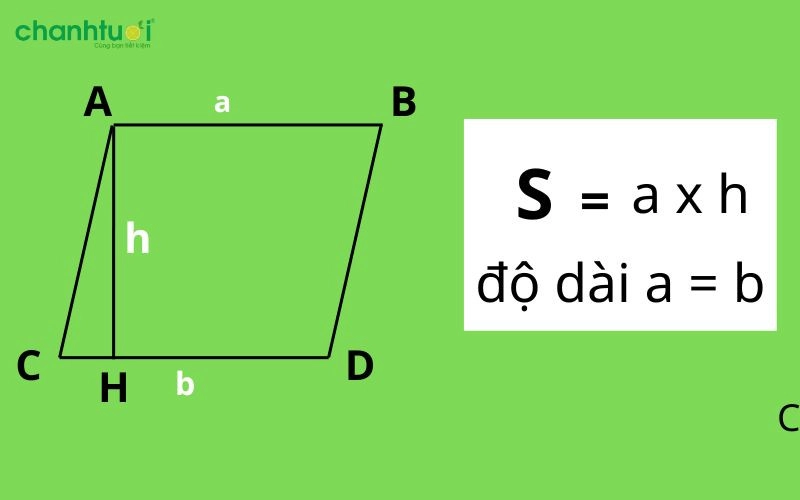Cách tính diện tích hình chữ nhật

Xem chi tiết tại đây: Công thích tính diện tích hình bình hành & các dạng bài tập

Công thức tính chu vi hình thang chính xác nhất

Để tính chu vi hình thang, công thức yêu cầu biết độ dài hai đáy và tổng chiều dài hai cạnh. Công thức tính chu vi hình thang là cộng tổng chiều dài hai đáy với độ dài cạnh gấp đôi.

Công thức tính chu vi hình thang:

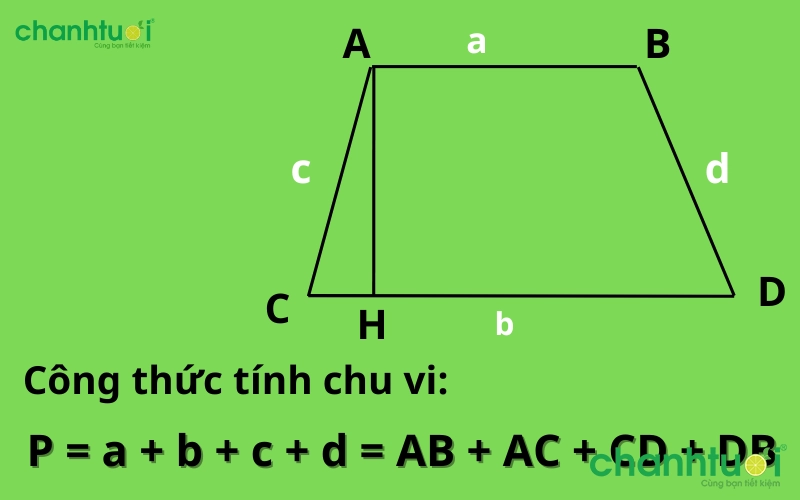Cách tính chu vi hình thang

• Chu vi hình thang = chiều dài đáy nhỏ + chiều dài đáy lớn + chiều dài cạnh 1 + chiều dài cạnh 2
• Cụ thể: P = a + b + c + d

Tính độ dài đáy của hình thang khi biết diện tích

Khi biết diện tích, chiều cao và chiều dài của một cạnh đáy, bạn cũng có thể tính được độ dài cạnh còn lại của hình thang.

Công thức: AB=2 x (S/h) – CD hoặc CD=2 x (S/h) – AB

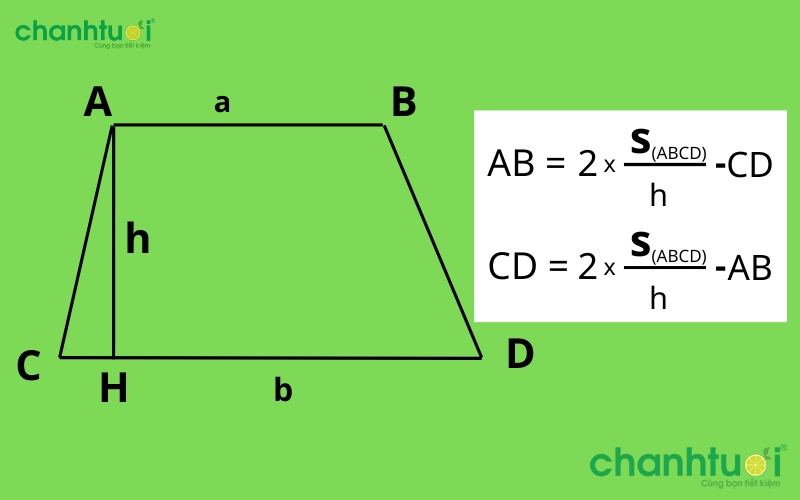Công thức tính đáy của hình thang

Ví dụ giải bài toán tính diện tích hình thang cụ thể

Bài 1: Tính diện tích hình thang khi biết: độ dài hai đáy lần lượt là 15cm và 14cm; chiều cao là 8 cm.

Áp dụng công thức S = ((a+b)/2) x h. Ta có: Diện tích hình thang là ((15 + 14)/2) x 8 = 116 cm2.

Bài học 2:

Có một mảnh đất hình thang có đáy nhỏ 20m, đáy lớn 25m. Mở rộng hai bên bên phải mảnh đất có đáy lớn hơn 5m và đáy nhỏ 3m để có được mảnh đất hình thang mới có diện tích lớn hơn diện tích ban đầu là 36m2. Tính diện tích mảnh đất hình thang ban đầu.

Phần thưởng:

Theo đầu bài, diện tích tăng thêm là diện tích hình thang có đáy lớn là 7m và đáy nhỏ là 5m. Do đó, chiều cao của thửa đất hình thang là: h = (36 x 2): (5 + 3) = 9m

Diện tích đất ban đầu là: S = 9 x (20 + 25): 2 = 202,5m²

Bài học 3:

Cho một hình thang vuông có khoảng cách giữa hai đáy là 16 cm thì đáy nhỏ bằng ¾ đáy lớn. Tính độ dài hai đáy khi biết diện tích hình thang vuông là 112cm2.

Phần thưởng:

Khoảng cách giữa hai đáy của một hình thang vuông là chiều cao của hình thang đó, vì vậy:

Tổng chiều dài của hai đáy là (112 x 2): 16 = 14cm

Gọi độ dài đáy nhỏ là a, độ dài đáy lớn b, ta có:

a + b = 14 và a = ¾ b

Vậy a = 14 x 4: 7 = 8cm

Do đó, đáy nhỏ = 34/7 cm, đáy lớn 64/7 cm

MUA BỘ QUY TẮC, ĐO BẰNG ĐỘ, SINH VIÊN EKE TẠI ĐÂY

5 bài tập tính diện tích hình thang không có đáp án

Bài tập 1: Cho hình thang ABCD. Bốn điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Biết diện tích tứ giác MNPQ là 135 cm2. Tính diện tích hình thang ABCD.

Bài 2: Cho hình thang ABCD có độ cao 4,2 m, diện tích = 36,12 m2 và đáy lớn CD dài hơn đáy nhỏ AB 7,8 m. Kéo dài AD và BC cắt nhau tại E. Biết AD = 3/5 DE. Diện tích tam giác ABE là bao nhiêu?

Bài 3: Cho hình thang ABCD có đáy nhỏ bằng 5m, đáy lớn bằng 8m và chiều cao bằng 6m. Tính diện tích của hình thang này.

Bài 4: Cho hình thang ABCD có đáy nhỏ là 6m, đáy lớn là 10m và chiều cao h là 5m. Tính diện tích hình thang.

Bài 5: Cho hình thang có diện tích là 120m2. Chiều dài và chiều cao h là 8m, cạnh đáy nhỏ là 4m. Tính độ dài cạnh đáy.

Xem thêm các công thức tính hình:

• Công thức tính độ cao chính xác nhất trong tam giác vuông, tam giác cân, đều, đều

Trên đây là hướng dẫn chi tiết công thức tính diện tích hình thang chính xác nhất. Hãy ghi lại để dễ nhớ hơn nhé!