[GIẢI] Các cách tìm ước chung lớn nhất ƯCLN nhanh nhất

Ước chung lớn nhất là gì? Cách tìm ước chung lớn nhất? bội số chung nhỏ nhất là gì? Đây là những kiến ​​thức toán học cơ bản quan trọng. Hãy theo dõi bài viết hôm nay của Chánh Tươi Review để hiểu rõ hơn về chủ đề này cũng như giải các bài toán về tìm ước chung, bội số chung nhé!

Cách tìm ước chung lớn nhất

Ước chung lớn nhất là gì?

Một điều ước là gì? Mong muốn chung là gì?

Trước khi tìm hiểu về ước chung lớn nhất, các bạn cần hiểu rõ ước số chung là gì và ước số chung là gì.

Số chia là gì: Nếu có một số tự nhiên a chia hết cho b thì ta nói b là ước của a. Tập hợp các ước số của a được ký hiệu là U(a).

Ví dụ: U(10) = {1; 2; 5; 10}; U(20) = {1; 2; 4; 5; 10; 20}

Yếu tố chung là gì: Yếu tố chung của hai hoặc nhiều số là yếu tố chung của tất cả các số đó. Ví dụ: nếu x là ước của số a và cũng là ước của số b thì x được gọi là ước chung của a và b. Ký hiệu là UC (a, b).

Ví dụ: UC(10, 20) = {1; 2; 5; 10}

Ước chung lớn nhất là gì?

Ước chung lớn nhất (ký hiệu là GCF) của hai hay nhiều số là số lớn nhất trong tập hợp ước chung của các số đó. Trong tiếng Anh, ước chung lớn nhất được gọi là ước chung lớn nhất (GCF).

• Ký hiệu ước chung lớn nhất của a và b là GCF(a, b).

Hãy sử dụng lại ví dụ mà Fresh Lemon Review đã sử dụng ở trên. U(10) = {1; 2; 5; 10}; U(20) = {1; 2; 4; 5; 10; 20} ta có tập UC(10, 20) = {1; 2; 5; 10} => GCF(10, 20) = 10.

Một ví dụ khác: Tìm GCF(24, 16, 32)

Chúng tôi có:

• U(24) = {1; 2; 3; 4; 6; 8; 12; 24}
• U(16) = {1; 2; 4; 8; 16}
• U(32) = {1; 2; 4; 8; 16; 32}
• UC(24, 16, 32) = {1; 2; 4; 8} => GCF(24; 16; 32) = 8

Cách tìm ước chung lớn nhất của hai số trở lên

Đối với bài toán tìm ước chung lớn nhất, bạn có thể áp dụng một trong các cách tìm ước chung lớn nhất dưới đây.

Cách tìm ước chung lớn nhất của 2 số trở lên

Cách 1: Liệt kê các ước chung của các số rồi chọn GCF

Để tìm ước chung lớn nhất của các số, chúng ta tìm tập hợp ước của mỗi số, sau đó tìm ước chung của các số đó và cuối cùng chọn ra ước chung lớn nhất. Đây là cách tôi đã áp dụng trong các ví dụ trên.

Thêm một ví dụ nữa để bạn dễ hình dung nhé!

Ví dụ: Tìm ước chung của số 6 và 12.

Bước 1: Tìm ước số tương ứng của số 6 và 12.

• Ta có: U(6) = {1; 2; 3; 6}; U(12) = {1; 2; 3; 4; 6; 12}

Bước 2: Tìm ước chung của số 6 và 12.

• Ta có: UC(6, 12) = {1; 2; 3; 6}

Bước 3: Chọn số HCLN trong số các ước chung.

• Chúng ta có GCF(6, 12) = 6

Cách 2: Phân tích số thành thừa số nguyên tố

Bạn làm theo từng bước một.

• Bước 1: Phân tích từng số thành thừa số nguyên tố.
• Bước 2: Chọn thừa số nguyên tố chung.
• Bước 3: Tạo tích của các thừa số đã chọn, mỗi thừa số được lấy với số mũ nhỏ nhất.
• Bước 4: Lấy sản phẩm chính là GCF mà bạn đang tìm kiếm.

Ví dụ: Tìm ước chung lớn nhất của các số 12 và 30.

Chúng tôi có:

Bước 1: Phân tích từng số thành thừa số nguyên tố của 12 và 30.

• Ta có: 12 = 2 x 2 x 3; 30 = 2 x 3 x 5

Bước 2: Chọn các thừa số nguyên tố chung của 12 và 30.

• Ta có: Hai thừa số nguyên tố chung là 2 và 3.

Bước 3: Biên dịch tích của các thừa số đã chọn, mỗi thừa số được lấy với số mũ nhỏ nhất.

• Ta có: 2 x 3 = 6

Bước 4: Lấy sản phẩm có GCF lần lượt là 12 và 30 mà bạn đang tìm kiếm.

• Vậy GCF(12, 30) = 6

Cách 3: Cách tìm ước chung lớn nhất theo bội số chung nhỏ nhất (BCNN) (điều kiện a, b khác 0)

Ước chung lớn nhất của a và b có thể được tính bằng cách chia tích của a và b cho bội chung nhỏ nhất của a và b.

Ví dụ: Tìm ước chung lớn nhất của các số 12 và 30.

(Lưu ý: Mình có hướng dẫn chi tiết cách tìm bội chung và bội chung nhỏ nhất ở phần dưới bài viết. Các bạn có thể xem chi tiết bên dưới để phương pháp tìm ước chung lớn nhất này dễ dàng hơn nhé!)

Chúng ta cần tìm bội số của mỗi số và tìm bội số chung nhỏ nhất (BCNN).

• B(12) = {0; 12; 24; 36; 48; 60,…}
• B(30) = {0; 30; 60,…}

Ta có: BCNN(12,30) = 60

• Chúng ta thực hiện phép tính bằng cách chia tích các số muốn tìm cho BCNN. Cụ thể (12:30):60 = 6.
• Do đó ta có GCF(12,30) = 6

Cách 4: Sử dụng thuật toán Euclide

Để tìm ước chung lớn nhất của hai số a và b bằng định lý Euclid, hãy làm theo các bước dưới đây.

Bước 1: Lấy số lớn chia cho số bé. Giả sử a > b, ta có phép tính (1) a:b

• Trường hợp 1: Nếu kết quả phép chia là số nguyên không có số dư => GCF(a, b) = b.
• Trường hợp 2: Nếu kết quả phép chia có số dư thì bạn chia số chia cho số dư. Lặp lại cho đến khi số dư = 0.

Bước 3: Khi phép chia cuối cùng có số dư = 0, => ước số cuối cùng là GCF(a, b).

Để giúp bạn đọc dễ hình dung hơn, tôi đưa ra ví dụ dưới đây:

Ví dụ: Tìm ước chung lớn nhất của 123 và 456.

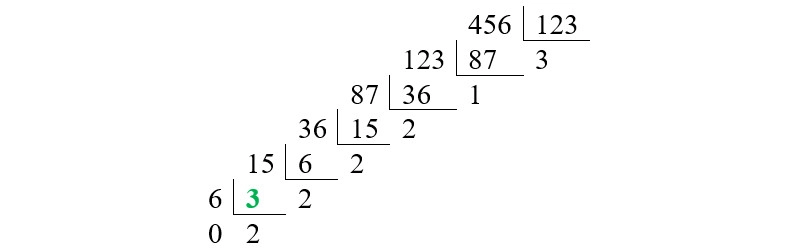Thực hiện tính toán tìm GCF theo định lý Euclid

Chúng tôi có:

• Bước 1: Lấy số lớn 456 chia cho số nhỏ 123.
• Bước 2: Kết quả của phép chia có số dư là 87. Ta lấy ước số của 123 chia cho số dư 87. Kết quả vẫn dư 36, tiếp tục lấy ước số của 87 chia cho phần còn lại của 36,… Lặp lại. Lặp lại cho đến khi cuối cùng số 6 chia cho số dư 3 cho kết quả là một số nguyên không có số dư.
• Bước 3: Khi số dư = 0, ta lấy số dư 3 cuối cùng làm GCF. Do đó: GCF(123, 456) = 3.

Cách 5: Sử dụng máy tính CASIO fx-580VN X

Bạn có thể thao tác nhanh chóng trên máy tính cầm tay CASIO fx-580VN X. Tính năng/phím “GCD” cho phép chúng ta tìm ước chung lớn nhất của hai số a và b một cách nhanh chóng và chính xác.

Bạn thực hiện các bước sau (tham khảo hướng dẫn trong ảnh): Tìm ước chung lớn nhất của 123 và 456.

Sử dụng CASIO fx-580VN

Mối quan hệ giữa ước số, ước số chung và ước số chung lớn nhất của hai số a và b:

Mối quan hệ giữa ước số, ước số chung và ước số chung lớn nhất của hai số a và b được biểu thị bằng biểu thức: UC(A, B)=UC(UCLN(a, b))

Ví dụ: GCF(8, 24) = 8

Vậy UC(8, 24) = U(8)= {1, 2, 4, 8}

Những điều cần lưu ý khi tìm ước chung lớn nhất

Trường hợp trong số các số cần tìm GCF có 1 số = 1 thì ước chung lớn nhất của các số đó bằng 1.

• Ví dụ: GCF(1; 55; 95) = 1

Nếu các số đã cho không có thừa số nguyên tố chung thì ước số chung lớn nhất của số đó là 1.

• Ví dụ: Số 5 và số 8 không có thừa số nguyên tố chung nên GCF(5, 8) = 1

Hai hoặc nhiều số có ước chung lớn nhất là 1 được gọi là số nguyên tố cùng nhau.

• Ví dụ: GCF(6, 35) = 1 nên 6 và 35 là số nguyên tố cùng nhau.

Trong các số đã cho, nếu có số nhỏ nhất là ước của các số còn lại thì ước chung lớn nhất của các số đã cho chính là số nhỏ nhất đó.

• Ví dụ: 5 là ước của 5 và 15 nên GCF(5, 15) = 5

Giải bài tập tìm ước chung lớn nhất

Dạng bài 1. Tìm ước chung lớn nhất của các số cho trước

Đây là dạng bài tập đơn giản nhất để tìm ước chung lớn nhất. Bài kiểm tra sẽ chỉ định 2 số trở lên và yêu cầu bạn tìm số GCF.

Với kiểu này bạn chọn 1 trong 5 cách tìm mà mình hướng dẫn ở trên để tìm ra số cần tìm.

Ví dụ:

• Tìm ước chung lớn nhất của các số 3, 6, 30. => GCF(3, 6, 30) = 3.
• Tìm ước chung lớn nhất của 5, 100. GCF(5, 100) = 5.
• Tìm GCF(30, 60). GCF(30, 60) = 30.

Bài 2: Tìm các số thành phần khi biết GCF hoặc các điều kiện khác.

Ví dụ: : Tìm ước chung của 12 và 30 bằng cách tìm GCF của hai số này.

Ta có: 12 = 2 x 2 x 3; 30 = 2 x 3 x 5

Vậy GCF(12, 30) = 2 x 3 = 6.

Áp dụng mối quan hệ giữa ước số, ước số chung và GCF. Chúng ta có UC(12, 30) = UC(6) = {1; 2; 3; 6}.

Loại vấn đề 3: Vấn đề có cách giải quyết

Ví dụ: Một hình chữ nhật có chiều dài 150m, chiều rộng 90m, được chia thành các hình vuông có diện tích bằng nhau. Tính độ dài cạnh hình vuông lớn nhất trong phép chia trên? (số đo cạnh là số tự nhiên có đơn vị là m)

Trả lời:

Để chia một hình chữ nhật thành các hình vuông có diện tích bằng nhau thì độ dài mỗi cạnh hình vuông phải là ước chung của 150 và 90. Do đó, độ dài cạnh hình vuông lớn nhất là GCF (90; 150) = 30.

Vậy độ dài cạnh lớn nhất của hình vuông là 30m

Cách tìm bội số chung nhỏ nhất

Cách tìm LCM của 2 số trở lên

bội số chung nhỏ nhất là gì?

Bội chung nhỏ nhất của a, b là số khác 0 nhỏ nhất trong tập hợp bội chung của a, b. Bội chung nhỏ nhất của hai số a và b được ký hiệu là [a,b] hoặc BCNN(a,b).

Một số trường hợp đặc biệt:

• Nếu 1 trong 2 số cần tìm = 1 thì LCM là số còn lại. => BCNN(a, 1) = a
• Nếu 1 trong 3 số trở lên cần tìm = 1 thì LCM là LCM của các số còn lại. => BCNN(a, b, 1) = BCNN(a, b).

Dưới đây là một ví dụ cụ thể:

• BCNN(5, 1) = 5
• BCNN(3, 9, 1) = BCNN(3, 9)

Cách tìm bội số chung nhỏ nhất

Để tìm LCM(a, b, c, …) bạn làm như sau.

• Bước 1: Phân tích các số thành thừa số nguyên tố.
• Bước 2: Bắt đầu chọn thừa số nguyên tố chung và thừa số nguyên tố riêng.
• Bước 3: Biên dịch tích các thừa số nguyên tố tìm được ở bước 2, mỗi thừa số sẽ lấy số mũ lớn nhất và tích đó là LCM cần tìm.

Dưới đây là ví dụ cụ thể: Tìm LCM(8, 18, 30)

Bước 1: Phân tích 3 số trên thành thừa số nguyên tố. Cụ thể:

• 8 = 2³
• 18 = 2 × 3²
• 30 = 2×3×5

Bước 2: Tiến hành chọn thừa số nguyên tố chung và thừa số nguyên tố riêng lần lượt là 2, 3 và 5. Lúc này số mũ lớn nhất của 2 là 3, số mũ của 3 là 2 và 5 sẽ là 1.

• Bước 3: Lúc này tích của các số đó sẽ là LCM của 8, 18, 30 sẽ là 2³ × 3² × 5 = 360 => LCM(8, 18, 30) = 360.

Chú ý:

• Trong trường hợp số đã cho là một cặp số nguyên tố thì LCM là tích của các số đó. Ví dụ: BCNN(5, 7, 8) = 5 × 7 × 8 = 280
• Trong trường hợp các số đã cho, nếu số lớn nhất là bội số của số còn lại thì LCM là số lớn nhất đó. Ví dụ: BCNN(12, 16, 48) = 48
• Chúng ta có thể tìm LCM(a, b) = ab
• Để tìm bội số chung của các số đã cho, chúng ta có thể tìm bội số LCM của các số đó.

Ví dụ về tìm bội số chung nhỏ nhất (BCNN)

Ví dụ 1: Tìm BCNN(20, 54)

Giải: Ta phân tích các số nguyên tố thành nhân tử:

• 20 = 2² x 5
• 54 = 2 x 3³
• BCNN(20x 54)= 2² x 3³ x 5 = 540

Ví dụ 2: Biết số học sinh của một trường có từ 400 đến 500 học sinh. Khi tập thể dục giữa lớp, xếp các hàng có số học sinh bằng nhau và thấy rằng 12 hàng, 15 hàng, 21 hàng đều đủ. Tính số học sinh của trường đó.

Giải: Ta rút ra thừa số nguyên tố: 12 = 2² x3 ; 15=3 x 5; 21 = 3 x 7

BCNN (12, 15. 21) = 2² x 3 x 5 x 7 = 420

BC(12, 15, 21) là bội số của BCNN(12, 15, 21)

⇒ BC(12, 15, 21) = B(420) = {0; 420; 840,……}

Số lượng học sinh 400 ≤ X 450

⇒ Số lượng học sinh là 420 học sinh.

Ví dụ 3: Tìm số tự nhiên nhỏ nhất khác 0 a biết a chia hết cho 15 và a chia hết cho 18.

Phần thưởng:

• a chia hết cho 15 và a chia hết cho 18 nên a là bội số chung của 15 và 18.
• a là số khác 0 nhỏ nhất nên suy ra: a là BCNN(15, 18) = 90.

Tìm ước số chung lớn nhất Python: Python là ngôn ngữ lập trình được sử dụng rộng rãi trong các ứng dụng web, phát triển phần mềm, khoa học dữ liệu và học máy (ML). Trong nội dung hôm nay mình chỉ chia sẻ cách giải bài toán tìm GCF lớp 6 cho học sinh và phụ huynh thông cảm nhé!

• Ước chung nhỏ nhất của mọi số là 1.
• Bội số chung lớn nhất của các số là vô hạn và không thể xác định được.

Bạn có thể xem thêm một số nội dung toán khác:

• Số thập phân là gì? Cấu trúc và cách đọc số thập phân?

Trên đây Chánh Tươi Review đã chia sẻ đến các bạn khái niệm và cách tìm ước chung lớn nhất và bội chung nhỏ nhất của 2 số trở lên bằng nhiều cách. Chúc bạn thành công!