Hướng dẫn cách giải phương trình bậc 2 & định lý Viet

Bạn cần hướng dẫn cách giải phương trình bậc hai cho học sinh lớp 8, lớp 9? Hãy cùng theo dõi bài viết hôm nay của Chánh Tươi Review để tìm hiểu chi tiết nhé! Trong bài viết này tôi sẽ giới thiệu rõ ràng về phương trình bậc hai, dạng toán và hướng dẫn giải các bài tập nổi bật. Xem ngay!

Phương trình bậc hai (một phương trình bậc hai chưa biết) là gì?

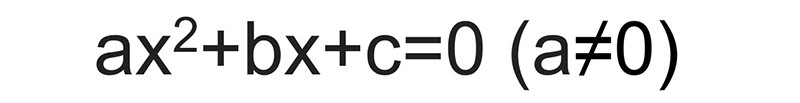Phương trình bậc hai có một ẩn số

Phương trình bậc hai (còn được gọi là phương trình bậc hai chưa biết) là phương trình có dạng: ax² +bx+c=0 (điều kiện a≠0) (1).

Trong đó:

• a, b, c gọi là các hệ số (a ≠ 0)
• x được gọi là ẩn

Giải phương trình bậc hai là tìm tất cả các giá trị của x thỏa mãn điều kiện khi thay x vào phương trình (1) thì ax² +bx+c=0.

Một số trường hợp phương trình bậc hai có một ẩn số:

Trường hợp 1: Khi số chưa biết a = 0

• Lúc này phương trình sẽ trở về dạng phương trình bậc nhất với 1 ẩn số có dạng bx + c = 0
• Ta có nghiệm của phương trình: x = -c/b

Trường hợp 2: Khi số chưa biết b = 0

• Bây giờ phương trình sẽ có dạng: ax² + c = 0
• Ta có nghiệm của phương trình: x = ±√(-c/a)

Trường hợp 3: Khi số chưa biết c = 0

• Bây giờ phương trình sẽ có dạng: ax² + bx = 0 ⇔ x(ax + b) = 0
• Ta có 2 nghiệm của phương trình: x = 0 và x = -b/a

Chi tiết về cách giải phương trình bậc hai

Cách giải phương trình bậc hai

Bước 1: Tính Δ=b²-4ac

Bước 2: So sánh Δ với 0

• Δ => phương trình (1) vô nghiệm
• Δ = 0 => phương trình (1) có nghiệm kép => x1 = x2 = -b/2a

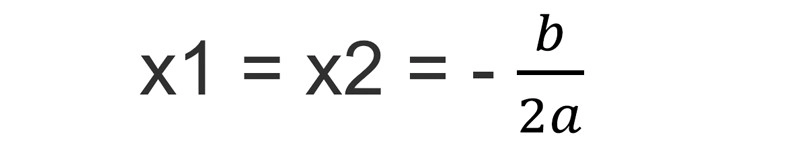Nghiệm của phương trình căn bậc hai có Δ = 0

• Δ > 0 => phương trình (1) có 2 nghiệm phân biệt, ta sử dụng công thức nghiệm sau:

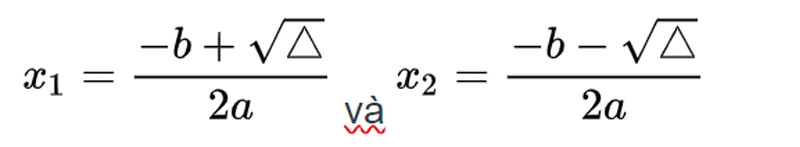Giải phương trình căn bậc hai với Δ > 0

Phân tích các yếu tố

• Nếu phương trình (1) có hai nghiệm x1, x2 phân biệt, bạn luôn có thể viết nó dưới dạng sau: ax² + bx + c = a(x-x1)(x-x2) = 0.
• Trở lại phương trình (2), sau khi tìm được 2 nghiệm x1, x2 ta viết được dưới dạng: 4(x-3/2)(x+1)=0.

Mẹo tính nhanh phương trình bậc hai:

• Nếu a+b+c=0 thì x1 = 1, x2 = c/a
• Nếu a-b+c=0 thì x1 = -1, x2 = -c/a

Định lý Việt giải phương trình bậc hai

Cho một phương trình bậc hai chưa biết (1). Giả sử phương trình có 2 nghiệm x1 và x2 thì thỏa mãn hệ thức sau:

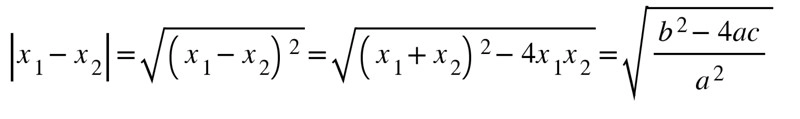Điều kiện thỏa mãn

Dựa vào hệ thống nêu trên, ta có thể sử dụng định lý Việt để tính các biểu thức đối xứng chứa x1 và x2.

• x1+x2=-b/a
• x1² +x2² =(x1+x2)² -2x1x2=(b² -2ac)/a²

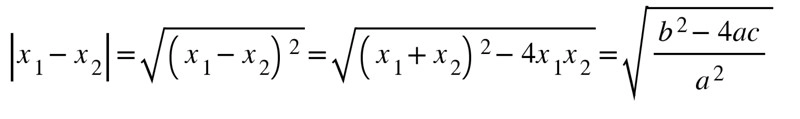Ứng dụng Việt trong phương trình bậc hai có một ẩn số

Nhận xét: Đối với dạng này, chúng ta cần thay đổi biểu thức sao cho (x1+x2) và x1x2 xuất hiện để áp dụng hệ thống tiếng Việt.

Định lý Converse Việt: Giả sử tồn tại hai số thực x1 và x2 thỏa mãn: x1+x2=S, x1x2=P thì x1 và x2 là 2 nghiệm của phương trình x2 -Sx+P=0.

Vận dụng định lý Việt để giải phương trình bậc hai có ẩn số

• Nhẩm nhẩm phương trình bậc hai: đưa ra phương trình ax² +bx+c=0 (a≠0),
  • Nếu a+b+c=0 thì phương trình có nghiệm x1=1 và x2=c/a
  • Nếu a-b+c=0 thì phương trình có nghiệm x1=-1 và x2=-c/a
• Phân tích nhân tử đa thức: đối với đa thức P(x)=ax2+bx+c nếu x1 và x2 là nghiệm của phương trình P(x)=0 thì đa thức P(x)=a(x-x1) (x-x2)
• Xác định dấu của nghiệm: đối với phương trình ax2 +bx+c=0 (a≠0), giả sử x1 và x2 là hai nghiệm của phương trình. Theo định lý Việt ta có:

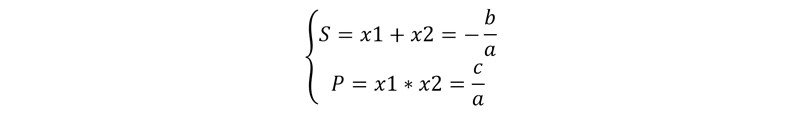Định lý Việt

• Nếu S
• Nếu S>0, x1 và x2 cùng dấu:
  • P>0 thì cả hai nghiệm đều dương.
  • P

Ví dụ bài tập giải phương trình bậc hai

Bài 1: Giải phương trình 4x² – 2x – 6 = 0 (2)

Δ=(-2)² – 4.4.(-6) = 4 + 96 = 100 > 0 => đã cho phương trình (2) có 2 nghiệm phân biệt.

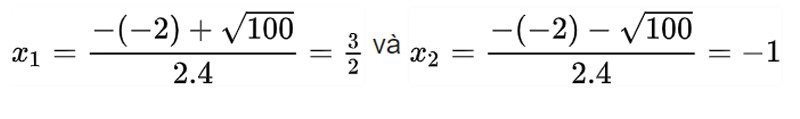Giải phương trình 4x² – 2x – 6 = 0

Bạn cũng có thể tính nhẩm nhanh vì bạn nhận ra rằng 4-(-2)+6=0, nên x1 = -1, x2 = -c/a = -(-6)/4=3/2. Cách giải quyết vẫn như trên.

Bài 2: Giải phương trình 2x² – 7x + 3 = 0 (3)

Tính Δ = (-7)² – 4.2.3 = 49 – 24= 25 > 0 => (3) có 2 nghiệm phân biệt:

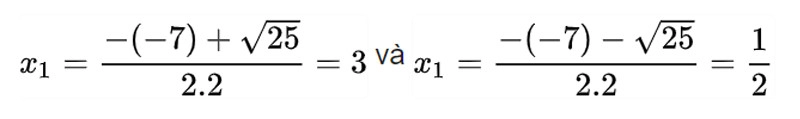Giải phương trình 2x² – 7x + 3 = 0

Để kiểm tra xem bạn đã tính đúng đáp án chưa rất dễ dàng, chỉ cần thay x1, x2 vào phương trình 3, nếu kết quả bằng 0 là chuẩn. Ví dụ: thay thế x1, 2,3²-7,3+3=0.

Bài 4: Giải phương trình 3x² + 2x + 5 = 0 (4)

Tính Δ = 2² – 4.3.5 = -56 phương trình (4) vô nghiệm.

Bài 5: Giải phương trình x² – 4x +4 = 0 (5)

Tính Δ = (-4)² – 4.4.1 = 0 => phương trình (5) có nghiệm kép:

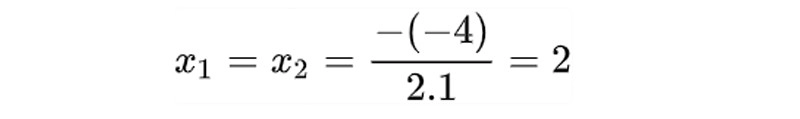Giải phương trình x2 – 4x +4 = 0

Trên thực tế, nếu suy nghĩ nhanh, bạn có thể thấy rằng đây là đẳng thức đáng nhớ (ab)2 = a2 – 2ab + b2, do đó rất dễ viết lại (5) thành (x-2)² = 0 x=2 .

Bài 6: Giải phương trình 4x^4-3²-1=0 (6) Phương trình chuyển về dạng bậc hai

Phương trình bậc hai: ax^4+bx²+c=0 (a≠0):

• Bước 1: Đặt t=x² (t ≥0).
• Bước 2: Phương trình đã cho có dạng: at2+bt+c=0
• Bước 3: Giải như phương trình bậc hai thông thường, chú ý điều kiện t ≥0

Lưu ý: phương pháp thiết lập t=x² (t ≥0) được gọi là phương pháp thiết lập ẩn thứ cấp. Ngoài việc đặt ẩn số phụ như trên, đối với một số bài toán cần khéo léo lựa chọn ẩn số phụ tốt nhất để đưa bài toán từ bậc cao về dạng bậc 2 quen thuộc. Ví dụ: bạn có thể đặt t=x+1, t=x2+x, t=x2-1…

Giải phương trình (6):

• Đặt t=x2 (t ≥0), lúc này phương trình trở thành:
• 4t²-3t-1=0, suy ra t=1 hoặc t=-¼
• t=1 ⇔ x2=1 ⇔ x=1 hoặc x=-1.
• t=-¼ , bị loại do điều kiện t ≥0
• Vậy phương trình có nghiệm x=1 hoặc x=-1.

[Mẹo] Máy tính giải phương trình bậc hai trực tuyến hoặc cách giải phương trình bậc hai trực tuyến các bạn có thể truy cập: https://technhanh.com/giai-phuong-trinh-bac-2.

Hy vọng những chia sẻ vừa qua đã giúp các bạn hiểu và thực hiện được các bài tập về cách giải phương trình bậc hai có ẩn số một cách dễ dàng và chính xác!