Tổng hợp công thức tính chu vi tam giác chính xác nhất

Các bạn đang học công thức tính chu vi hình tam giác đều và các hình đặc biệt hơn như tam giác vuông, tam giác cân hoặc tam giác đều. Hãy theo dõi bài viết hôm nay cùng Fresh Lemon Review để tìm hiểu chi tiết nhé! Đây là công thức toán rất quan trọng trong việc giải các bài tập toán hình học cũng như ứng dụng thực tế sau này trong cuộc sống. Đừng bỏ lỡ nó!

Giới thiệu về hình tam giác

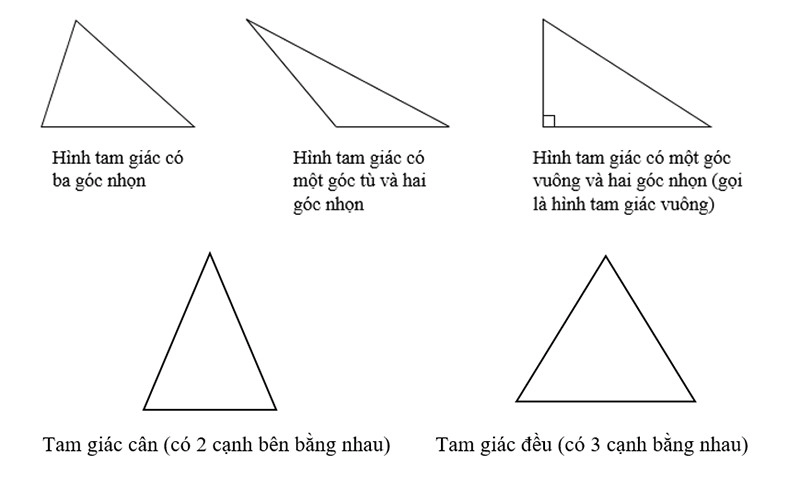Mô tả các loại hình tam giác

Tam giác là một hình học cơ bản quan trọng trong lĩnh vực toán học và hình học, được xác định bởi sự hiện diện của ba cạnh và ba đỉnh. Đối với hình tam giác có nhiều loại khác nhau như tam giác đều, tam giác cân, tam giác vuông, tam giác nhọn và tam giác tù. Việc phân loại tam giác có thể dựa vào đặc điểm các cạnh và các góc để xác định loại cụ thể.

Bạn có thể tìm hiểu thêm về đặc điểm của hình tam giác tại đây: “Giới thiệu về hình tam giác” – Trong bài Các công thức tính diện tích hình tam giác chính xác nhất.

XEM SHOP CHUYÊN DỤNG CỤ HỌC TẬP UY TÍN TẠI ĐÂY

Tổng hợp công thức tính chu vi hình tam giác chính xác nhất

Với mỗi loại tam giác cụ thể, chúng ta sẽ áp dụng các công thức tính chu vi khác nhau. Cụ thể công thức tính chu vi của từng loại tam giác được trình bày như sau.

Công thức tính chu vi hình tam giác đều

Hình tam giác thường là hình tam giác cơ bản và phổ biến nhất mà học sinh thường gặp. Nó được đặc trưng bởi có các góc và cạnh không đồng đều.

Theo đó, chu vi của một tam giác sẽ được tính bằng tổng chiều dài 3 cạnh của tam giác đó. Ta có công thức: P = a + b + c

Trong đó:

• P: chu vi tam giáca, b, c: độ dài ba cạnh của tam giác

Minh họa:

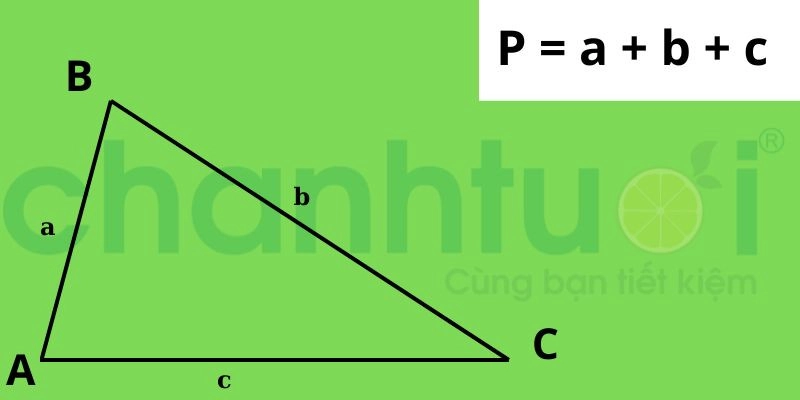Cách tính chu vi của một hình tam giác đều

Ví dụ: Cho tam giác ABC có độ dài ba cạnh AB, AC, BC lần lượt là 3cm, 4cm và 6cm. Tính chu vi của một hình tam giác?

Giải: P(ABC) = 3 + 4 + 6 = 13cm.

Công thức tính chu vi của một tam giác vuông

Tam giác vuông là tam giác có một góc bằng 90 độ. Xét công thức tính chu vi tương tự như cách tính một tam giác đều, chu vi bằng tổng độ dài 3 cạnh của tam giác đó. Ta có công thức tính chu vi tam giác vuông: P = a + b + c

Trong đó:

• P: chu vi của tam giác vuông
• a, c: độ dài hai cạnh của một tam giác vuông
• b: độ dài cạnh huyền của tam giác vuông

Hình minh họa:

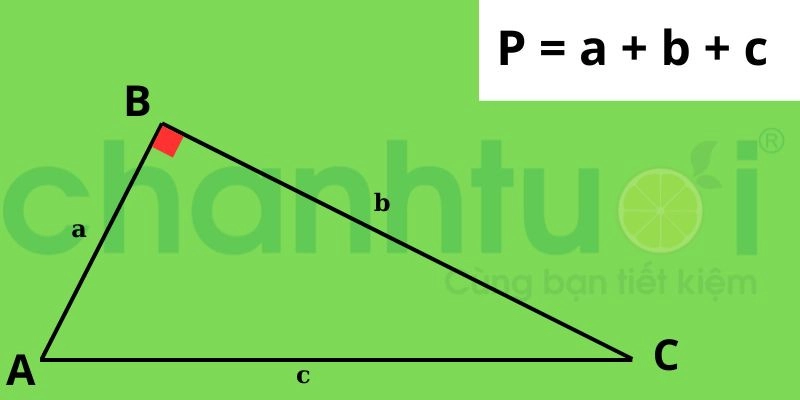Cách tính chu vi của một tam giác vuông

Ví dụ: Cho tam giác vuông ABC có độ dài 3 cạnh AB = 2 cm, AC = 5 cm, BC = 6 cm. Tính chu vi của một tam giác vuông?

Giải: P(ABC) = 2 + 5 + 6 = 13cm.

Công thức tính chu vi của một tam giác cân

Điểm đặc biệt của tam giác cân là 2 cạnh và 2 góc trong tam giác bằng nhau. Khi đó công thức tính chu vi là P = 2.a + c

Trong đó:

• P: chu vi tam giác
• a: độ dài hai cạnh của một tam giác cân
• c: độ dài cạnh đáy của tam giác cân

Hình minh họa:

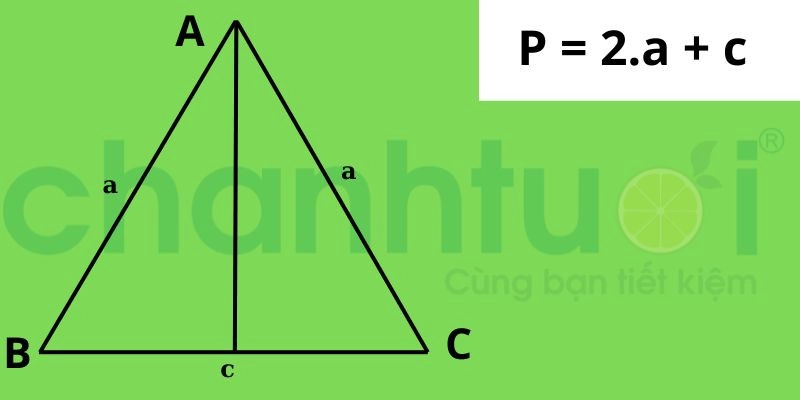Cách tính chu vi của một tam giác cân

Ví dụ: Cho tam giác cân có cạnh AB = AC = 3cm. Cạnh đáy BC = 4 cm.. Tính chu vi tam giác cân ABC?

Giải: P (ABC) = 2*3 + 4 = 10cm.

Công thức tính chu vi của tam giác vuông cân

Tam giác vuông cân là một loại tam giác đặc biệt có tính chất của cả hai loại tam giác: tam giác cân và tam giác cân. Theo đó, một tam giác vuông cân sẽ có hai cạnh góc vuông có độ dài bằng nhau và hai góc nhọn có số đo 45 độ.

Ta có công thức tính chu vi tam giác vuông cân: P = 2a + c

Trong đó:

• P: chu vi của tam giác vuông cân
• a: độ dài hai cạnh của tam giác vuông cân
• c: độ dài cạnh đáy của tam giác vuông cân

Hình minh họa:

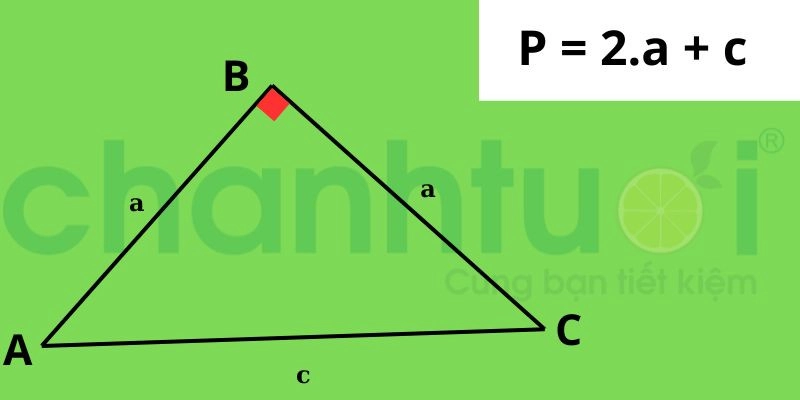Cách tính chu vi của một tam giác vuông cân

Ví dụ: Cho tam giác vuông cân ABC có cạnh AB = AC = 4 cm. Cạnh đáy BC = 5 cm. Tính chu vi tam giác vuông cân ABC?

Giải: P (ABC) = 2*5 + 5 = 15 cm.

Công thức tính chu vi của một tam giác đều

Tam giác đều là tam giác đặc biệt có ba cạnh và ba góc nhọn bằng nhau. Đây cũng là trường hợp đặc biệt của tam giác cân. Ta có công thức tính chu vi tam giác đều: P = a + a + a = 3 xa

Trong đó:

• P: chu vi của một tam giác đều
• a: độ dài cạnh của một tam giác đều

Hình minh họa:

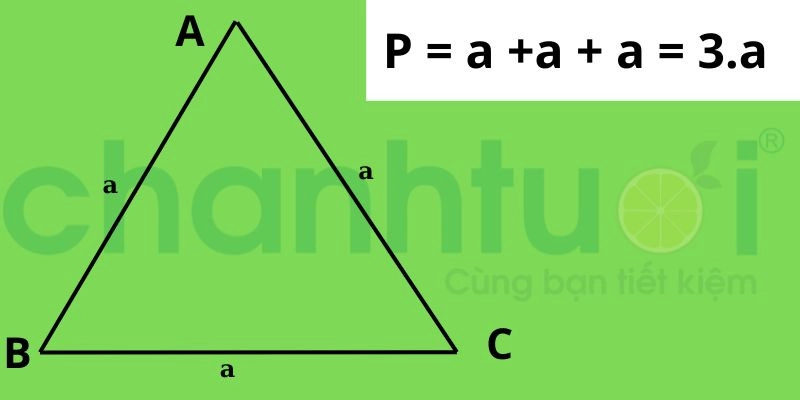Cách tính chu vi tam giác đều có 3 cạnh bằng nhau

Ví dụ: Cho tam giác đều ABC có độ dài cạnh AB = AC = BC = 4 cm. Tính chu vi tam giác đều ABC?

Giải: P (ABC) = 3*4 = 12 cm.

Cách tính chu vi hình tam giác trong không gian

Giả sử bạn gặp một bài toán cần tính chu vi của một hình tam giác trong không gian như sau:

Bài toán: Trong không gian có mặt phẳng Oxy, xét hai điểm A(1;3) và B(4;2).

1. Tìm tọa độ điểm D trên trục Ox sao cho DA = DB;

2. Tính chu vi tam giác OAB;

3. Tính chu vi hình tam giác trong không gian.

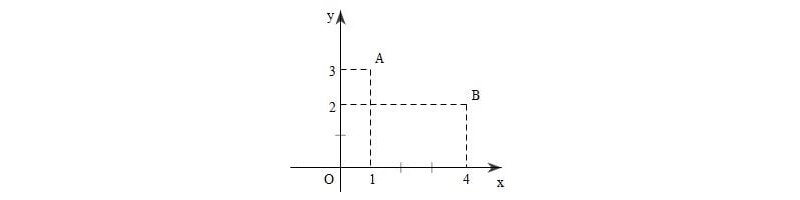Vẽ tọa độ trong không gian

Đây là giải pháp cho vấn đề trên:

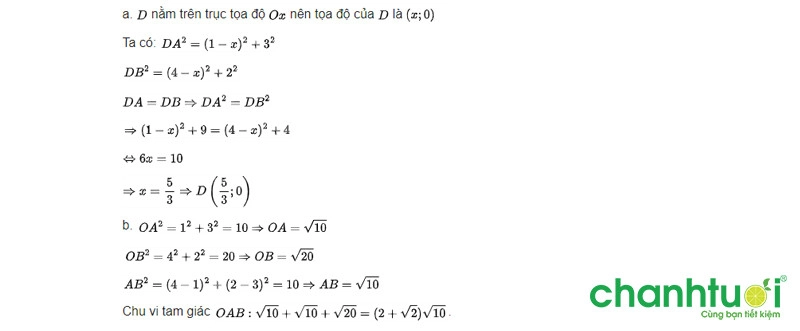Giải bài tập tính chu vi hình tam giác trong không gian

Cách tính một nửa chu vi của hình tam giác

Cho tam giác ABC có độ dài ba cạnh AB, AC, BC lần lượt là a, b, c. Ta có công thức tính nửa chu vi tam giác ABC bằng tổng chiều dài 3 cạnh của tam giác chia làm đôi.

Gọi p là nửa chu vi của tam giác. Ta có p = P : 2 = (a + b + c) : 2.

Ví dụ: Cho tam giác ABC có độ dài ba cạnh là 3 cm, 5 cm, 6 cm. Tính nửa chu vi tam giác ABC.

Ta có: p = (3 + 5 + 6): 2 = 7 cm.

Bài tập áp dụng công thức tính diện tích tam giác

Bài tập 1

Cho một tam giác có các cạnh lần lượt là 3 cm, 5 cm và 7 cm, chu vi của tam giác này là bao nhiêu:

Hồi đáp:

• Áp dụng công thức P= a + b + c
• Do đó P = 3 + 5 + 7 = 15 cm.
• Vậy chu vi của tam giác đã cho là 15cm

Bài tập 2

Tìm độ dài cạnh c nếu P = 30 cm và a = 8 và b = 10 cm

Hồi đáp:

• Áp dụng công thức: P = a + b + c, thay các số đã cho vào công thức thành P=30, a=8 và b = 10. Thay chúng vào công thức ta được.
• 30 = 8+ 10+ c
• 30 = 18 + c
• Do đó, c = 12cm

Bài tập 3

Độ dài cạnh của tam giác cân sau đây tính bằng cm là bao nhiêu, biết độ dài cạnh không bằng nhau là 5cm và chu vi là 17cm?

Hồi đáp:

• Vì bài toán là tam giác cân nên độ dài hai cạnh còn lại sẽ bằng nhau (áp dụng tính chất của tam giác cân). Đặt độ dài mỗi cạnh bằng đơn vị: a
• Do đó, chu vi của tam giác cân đã cho sẽ được tính theo công thức P = a + a + 5
• Vì chu vi = 17cm nên ta có công thức tính như sau:
• 17 = 2a + 5
• 2a + 5 = 17
• 2a = 12
• một = 6cm
• Vậy độ dài các cạnh bằng nhau của một tam giác cân là 6cm.

Bài tập 4

Tam giác vuông cân là ABC có hai cạnh lần lượt là 3cm và 4cm. Biết rằng cạnh còn lại của tam giác gấp 2 lần tổng hai cạnh còn lại của tam giác. Tính chu vi tam giác ABC.

Hồi đáp:

• Theo bài học, ta có: AB = 3cm, AC = 4cm và BC = 2 (AB + AC)
• Vậy độ dài cạnh còn lại của tam giác là: BC = 2 (AB + AC) = 14 cm
• Chu vi tam giác ABC lúc này sẽ bằng: P(ABC) = AB + AC + BC = 3 + 4 + 14 = 19cm

Bài tập 5

Cho tam giác vuông ABC có 2 góc vuông AB=6cm, AC=8cm lần lượt. Tính chu vi tam giác vuông ABC?

Hồi đáp:

• Ta có: Tam giác ABC vuông tại A vì có 2 cạnh vuông là AB và AC nên BC là cạnh huyền của một tam giác vuông và BC=10 cm.
• Chu vi tam giác ABC là:
• P= AB +AC +BC= 6 + 8 + 10= 24cm
• Vậy chu vi tam giác vuông ABC đã cho là 24cm

Bài tập 6

Cho tam giác cân ABC tại A có cạnh AB = 4 cm, cạnh BC dài hơn cạnh AB 2 cm. Chu vi của tam giác cân ABC là bao nhiêu?

Hồi đáp:

• Độ dài cạnh BC là:
• 4 + 2= 6 (cm)
• Chu vi của tam giác cân ABC là:
• P= 2xa + c= 2x 4 + 7 = 15 (cm)
• Vậy chu vi tam giác cân ABC là 15 cm

MUA BỘ QUY TẮC, ĐO BẰNG ĐỘ, SINH VIÊN EKE TẠI ĐÂY

Bạn cũng có thể quan tâm đến cách tính diện tích hình thang:

• Công thức tính diện tích hình thang chính xác nhất

Như vậy Chánh Tươi Review vừa hướng dẫn các bạn chi tiết từng công thức tính chu vi tam giác đều, vuông, cân, cân, đều,… Cảm ơn các bạn đã theo dõi!